作者:王军辉
前言
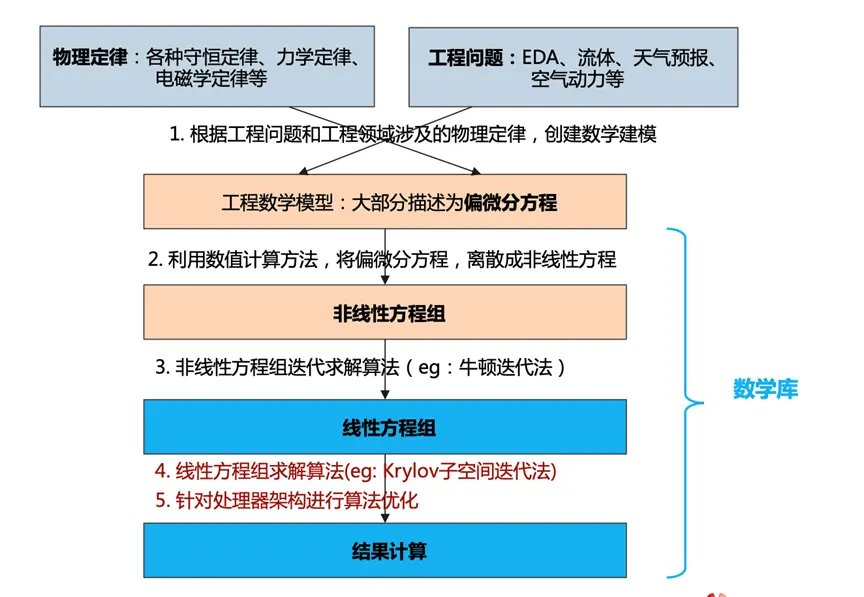
数学计算库是使能处理器在数值计算领域的基础软件库,是工程计算、科学计算、AI计算的基石。大部分物理、工程问题都能转化成线性方程组求解问题,而高效的数学计算库是发挥硬件算力的基石。
以BLAS(Basic Linear Algebra Subprograms,基本线性代数运算函数库的标准)为例。BLAS最早是由美国能源部(Department of Energy)于1979年发布的。在此之前,每个应用程序都需要手动实现线性代数算法,而这些算法又需要不同的数据结构和运算方式。
为了解决这个问题,美国能源部创建了BLAS标准,通过为常见操作(如向量乘法、矩阵乘法、向量加法等)定义通用接口,使得用户可以在不同的平台和计算机架构上重用相同的代码。最初的BLAS标准包含40个Fortran语言函数,用于执行常见的线性代数运算。
随着时间的推移,标准还进行了更新和扩充,增加了更多的函数和特性。BLAS已经成为一个广泛使用的标准,能够提供高效的线性代数运算,同时也是很多高性能库的基础,如OpenBLAS、MKL等。
随着计算机技术的发展和日益广泛的应用,数学计算库也不断演进,常用函数已经达到一万个,版本多种多样,也成为国际巨头掌控软件生态的关键手段。
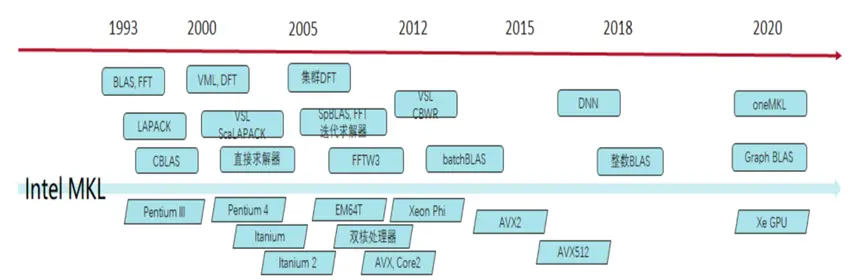
Intel MKL数学计算库发展时间轴
高性能数学计算库的现状
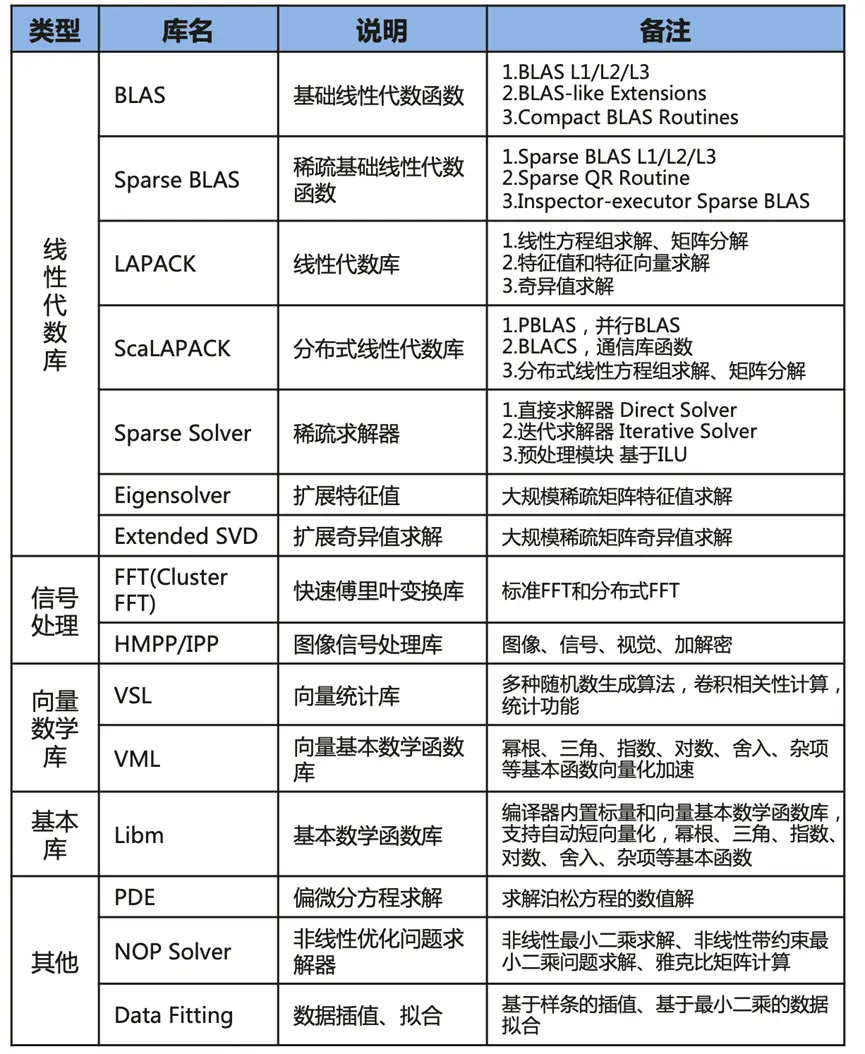
数学计算库主要包括线性代数库、信号处理、向量数学库、基本数学函数库(Libm)、PDE各种Solver,其大致范围参见“附件1”。
软件版本也多种多样,有专注于领域的数学计算软件,也有服务于某类处理器的数学计算软件,其他差异性还表现在以下几个方面:
- 服务于处理器的基础数学计算库版本。Intel的MKL数学计算库,只支持x86,源代码不开源,并优先支持Intel处理器,同时在x86生态,MKL库的使用也最为广泛,原因主要是发展早,以及Intel处理器在高性能计算领域的市场占有率极高有关。华为的KML数学计算库支持华为鲲鹏ARM处理器,不开源,按照“鲲鹏应用使能套件BoostKit许可协议”描述,仅面向签署该协议或者在鲲鹏硬件授权使用该软件包。澎峰科技的PerfMPL已经支持了多种主流指令集,如RISC-V、x86、ARM、RISC-V等指令集,并面向领域提供定向优化版本,商业版本不开源。还有CUDA这类的GPU并行数学计算库(cuBLAS、cuFFT等),用于NVIDA的GPU卡编程,其他公司是否可以使用CUDA计算库,法律授权存疑。
- 服务于领域的数学计算软件。例如,世界知名的开源项目OpenBLAS提供BLAS运算能力;FFTW实现快速傅里叶变换(Fast Fourier Transform);LAPACK(Linear Algebra Package)提供高级线性代数算法,如矩阵分解、特征值和特征向量计算等;VSIPL主要用于向量、信号和图像处理库;PETSc则提供更丰富一些的功能,如非线性求解、最优化、离散事件模拟和信号处理等。实际上,可以称之为数学计算库或者计算中间件的软件还有许多。
- 其他需要关注的差异性:
- 各种数学计算库软件存在开源、闭源的差异性。处理器公司自主开发的数学计算库通常是闭源,即使是可以使用,也随时面临版权拥有方授权协议的变化和制约。某些开源库协议商用不友好(例如FFTW是GPL协议,使用会导致产品所有代码被感染,将面临被迫开源)。
- 计算性能和计算精度问题,这两点在高性能计算领域尤其关注。所以,在使用开源软件作为商业服务的一部分时,需要重视。
- 支持的编程语言存在差异。OpenBLAS除支持C和C++以外,还支持Fortran、Python、R、Julia、MATLAB、Java等编程语言。
- 支持的操作系统存在差异。Intel MKL支持Windows、Linux、macOS;OpenBLAS支持Linux,macOS,Windows,BSD,Android/iOS;华为KML主要支持Linux相关操作系统。
发达国家都将并行化的数学计算库作为其基础软件的长期发展重点。例如:1993年,受到高性能计算机系统上的并行计算需求的推动,PETSc(Portable, Extensible Toolkit for Scientific Computation)项目正式启动,由美国加州大学圣巴巴拉分校计算科学研究所的数学和计算科学研究组(Mathematics and Computer Science group of the Institute for Computational Sciences)发起和开发,目的是为了提供一套并行的数学软件库,用于高效地解决大规模科学计算的问题。
现在,PETSc被广泛地应用于涡流,油藏模拟,光电学,电磁学,地震学,心脏模拟,碰撞模拟,天文学,机器学习等研究领域。
数学计算库的研发与发展,对一个国家在芯片设计、算法开发和应用场景多产生着非常积极的意义和重要的作用。
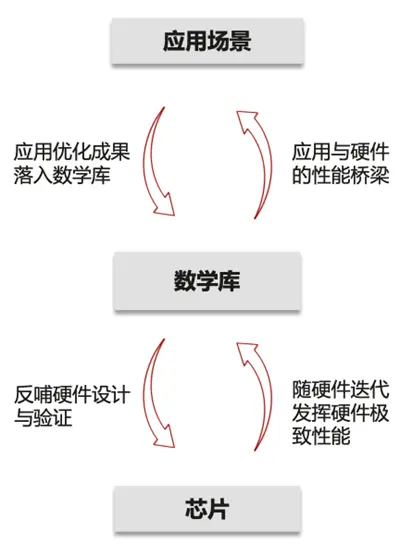
软硬融合发展示意图
高性能数学计算库的应用
高性能数学计算库对EDA、CAE、微电子工程等工程计算领域,发挥着重要的作用,支持并行计算和异构计算的数学计算库也是近年来的研究重点,如:
- 利用CPU的加速指令集进行算法加速。
- GPU并行算法加速
- 大规模集群并行计算
长期以来,国外为了控制我国高科技领域的发展,限制高性能的计算软件向中国用户提供。高性能数学计算库推动着科学研究的进步,也制约工程应用的效率。以下以几个典型的领域,介绍高性能数学计算库对应用的重要意义。
【CFD软件】线性代数库:用于解方程组,如求解矩阵方程和求解特征值和特征向量。最优化库:用于优化CFD模拟计算的效率和准确度。数值积分库:用于对数学函数进行数值积分,如有限差分方法。随机数生成库:用于产生随机数,这在许多CFD应用中是必要的。偏微分方程(PDE)求解库:用于求解一些非线性PDEs,如Navier-Stokes方程和热传递方程等。
【CAE软件】建模和仿真:数学计算库能够提供各种模拟算法和数值方法,如有限元法、有限差分法等,用于建模和仿真机械、电气、力学、热力学等领域的物理现象。优化设计:数学计算库提供各种优化算法,如遗传算法、模拟退火算法等,用于对CAE仿真模型进行设计和优化,以获得更好的性能和效率。数据分析:数学计算库提供各种数学函数和统计算法,用于分析和处理模拟数据,以获得有用的信息和洞见。机器学习:数学计算库中还提供了机器学习和数据挖掘的算法和工具,这些技术可以用于优化CAE仿真模型、识别模拟数据中的模式和异常,从而帮助工程师更好地理解和改进设计。
【微电子工程】计算光刻方法是一种通过计算机控制产生高分辨率图案的加工工艺,使用光刻光刻机将外源干涉光栅(如二极管激光器)的输出通过透镜等光学元件照射到硅晶圆表面上,然后进行化学及物理反应生成微电子芯片的微电路。数学计算库发挥着重要的作用。
- 模型建立:计算光刻涉及到光学、物理、化学等多个领域的知识,需要使用数学模型进行问题的数值求解。数学计算库可以提供各种数值计算算法和快速计算技术,如有限差分法、有限元法等,以建立可靠的计算模型。
- 仿真计算:数学计算库可以处理大量的数据和复杂的计算任务,可以在短时间内对整个光刻过程进行仿真计算,从而预测和优化光刻过程的各个环节。
- 优化设计:计算光刻涉及到的问题非常复杂,需要通过优化设计来提高制造效率和芯片质量。数学计算库可以提供各种优化算法,如遗传算法、粒子群算法等,以提高光刻制造的效率和芯片质量。
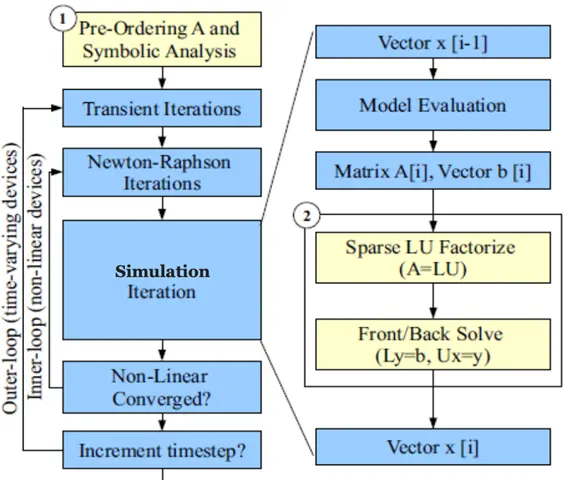
【EDA领域】在电路仿真中Sparse LU Factorize(稀疏LU分解)占到仿真时间的70%,小规模矩阵计算的优化可以提升计算效率。
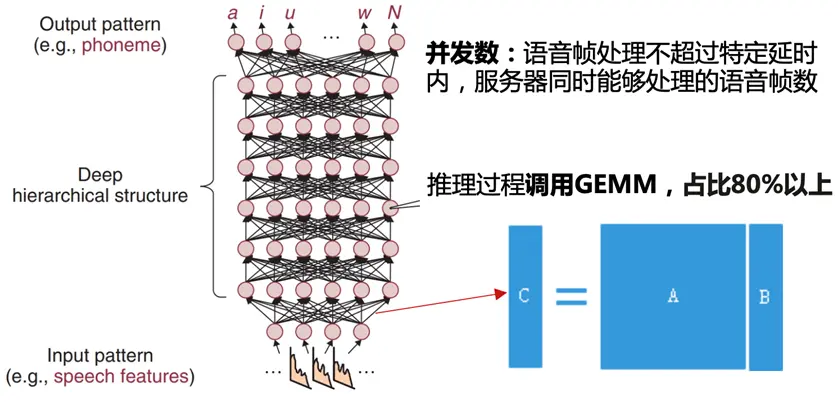
【AI领域】以语音识别的DNN推理为例,推理过程调用GEMM占比80%以上。通过对OpenBLAS的GEMM部分优化,发挥SIMD、多核并发,计算性能提高26%以上。
国产高性能数学计算库PerfMPL
张先轶(中科院博士)于2011年发起OpenBLAS开源项目,OpenBLAS是一个优化的BLAS库(http://www.openblas.net),被广泛应用于科学计算、数据分析、深度学习算法、人工智能等领域,被Caffe、MXNet、Julia、Ubuntu、Debian、openSUSE、GNU Octave等知名项目集成;OpenBLAS也被用作为各种处理器系统开发包的基础软件之一。
PerfMPL是以OpenBLAS为发展基础,经过多年发展逐步覆盖至FFT(快速傅立叶变换)、SPARSE(稀疏矩阵计算库)、MATH(基础数学库)、VML(Vector Math Library向量数学库)、DNN(Deep Neural Networks深度神经网络)、PerfIPP(图像处理等)等计算库。

PerfMPL基于澎峰科技拥有自主知识产权的统一数学函数库技术积累,通过针对性优化、完善、裁剪等方式,发展出两大分支版本:
- PerfMPL for 通用算力,主要面向CPU指令集。重点支持x86、ARM和RISC-V高性能通用处理器平台。
- PerfMPL for 专用算力,主要面向GPU、NPU、ASIC、FPGA和各类DSA。
自主研发的源代码,也使得澎峰科技可以为特定领域提供加速计算服务和领域数学计算库,并重点支持国产的CAE、EDA、信号处理、计算光刻等领域。
澎峰科技的软件加速计算理论体系是:模型制导、算法支撑、优化支持、性能为王,具体到PerfMPL而言:
PerfMPL主要优化策略如下
- 性能驱动的优化模型构建技术
- 面向复杂体系结构的新型并行算法设计
- 基于模板的高性能汇编代码自动生成技术
- 场景和应用感知兼顾的性能自适应优化技术
结束语
总的来说,高性能数学库已经经历了多个阶段的发展和演变,并且随着计算机硬件技术的不断提升,数学库的功能和效率也在不断地提高。从最初的基础数学函数库到现在能够进行复杂科学计算的数值计算库,高性能数学库的发展为科学计算和工程应用提供了强大的支持。
未来,我们可以期待更高效、更智能的数学库的诞生,这将会为解决更为复杂的问题提供更好的工具和支持。此外,高性能数学库的发展也在国家自主可控战略方针中扮演着重要的角色。
在当前全球科技创新竞争日益激烈的背景下,高性能数学库的自主研发和掌握,对于保障国家信息安全、提高关键技术自主可控能力和推动经济发展具有十分重要的战略意义。我们相信,在政府和企业共同努力下,高性能数学库的发展将在国家自主可控战略的支持下迈上新的台阶。
附件1: